Quest
Bienvenue !
Ce court tutoriel vous guidera à travers toutes les fonctionnalités de cette application.
Si vous desirez quitter cette application, cliquer sur la composante rorative en haut a droite. Sinon, continuez à défiler vers le bas.
En quoi consiste Quest ?
Cette application est basé sur la theorie des graphs. La composante principale est une grille en deux dimensions qui represente un graph avec des noeuds(vertices) reliés par des arêtes(edges). Le graph est non-orienté(undirected graph) c-à-d que les arêtes sont bidirectionnelles. Chaque carré dans la figure de gauche équivaut à un noeud dans la figure de droite.

Applications dans la vie réelle ?
Les graphiques sont directement applicables aux scénarios du monde réel. Par exemple, nous pourrions utiliser des graphiques pour modéliser un réseau de transport où les nœuds représenteraient les installations qui envoient ou reçoivent des produits et les bords représenteraient des routes ou des chemins qui les relient (voir ci-dessous). Dans le réseau de vol, les structures de données graphiques sont utilisées pour calculer les trajets les plus courts et la consommation de carburant dans la planification d'itinéraire.
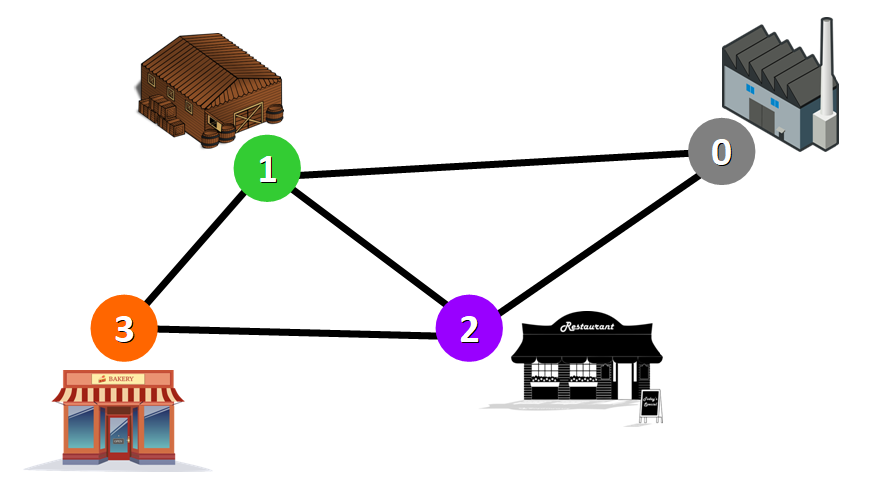
Chemin le plus optimale
La premiere fonction de base de Quest est de trouver le chemin le plus optimale entre deux points. C-à-d le chemin le moins coûteux en terme de ressources. Chaque deplacement dans n'importe quelle direction a de base un coût de 1, mais il est possible d'ajouter des obstacles / recomponses pour changer le coût du deplacement. Les algorithmes de recherches implementés permettent de visualiser le processus.

liste des Algorithmes de recherches
Breadth-first search :Un algorithme non-pondéréqui garantit le chemin optimal.
Depth-first search :Un algorithme non-pondéréqui ne garantit pas le chemin optimal.
Dijkstra :Un algorithme pondéréqui garantit le chemin optimal.
A* :Un algorithme pondéréqui garantit le chemin optimal. Il a commme spécificité d'utiliser des heuristiques, fonctions qui estiment a priori le coût minimum entre un noeud n vers le noeud final. Il est important de choisir des heuristiques qui sont admissibles.
Bellman Ford :Un algorithme pondéré.Il a dans son analyse comme spécificitée de aussi prendre en consideration les noeuds à valeurs negatives ou inferieur à 1 afin de garantir un chemin optimal. Il permet en plus de de detecter des cycles negatifs infinie.
Iterative deepening depth for search :Un algorithme non-pondéré,il n'est pas optimal dans un graph non-orienteé (undirected). L'algorithme est exécutée à plusieurs reprises avec des limites de profondeur croissantes jusqu'à ce que l'objectif soit trouvé. Il a comme capacité d'utiliser beaucoup moins de mémoire que BFS ou DFS, dans d'autres type de graphs/arbes. Dans notre cas (undirected graph), j'ai du modifer l'algorithme afin qu'il puisse garder en memoire les noeuds visités a chaque depth level afin d'eviter les cycles infinies, le rendant non-optimal.
Iterative deepening A* :Un algorithme pondéré,il n'est pas optimal dans un graph non-orienteé (undirected). L'algorithme une combinaison de A* et IDDFS, au lieu d'utiliser des "depth level" on utilise des "cost threshold" basé sur f(n)=g(n)+h(n). Ensuite, nous étendons les nœuds c qui satisfont f(c) < T. Tout comme IDDFS, l'algorithme a été modifé pour ce conformer a un graph non-orienteé, le rendant non-optimal.
Greedy best-first search / Weighted Greedy best-first search :Sont respectivement des algorithmes non-pondéré et pondéré.Ils sont des versions plus rapide et plus basé sur les heuristiques que A*. Mais, ils ne garantissent pas le chemin optimale.
Fonctionnalités
Vous pouvez ajouter des murs en cliquant sur la grille. Ajouter des poids(coût ≥ 1) en cliquant sur la grille pendant que vous maintenez la touche ALT. Ajouter des recompenses(-0.99 ≤ coût ≤ 0.99) en cliquant sur la grille pendant que vous maintenez la touche CTRL.
Les murs sont impénétrables, ce qui signifie qu'un chemin ne peut pas les traverser. Les poids et les recompenses, cependant, ne sont pas infranchissables. Les poids sont plus coûteux à traverser et les récompenses reduisent les coûts de traversées.

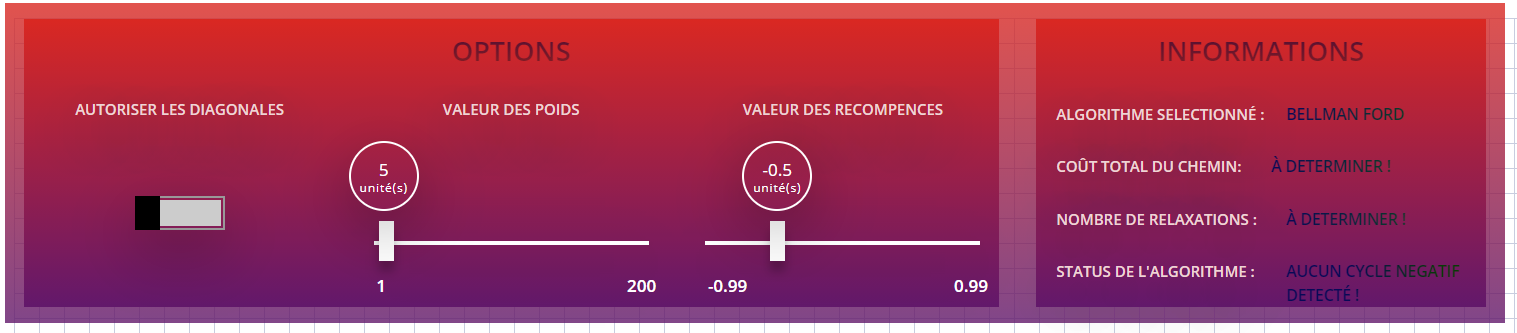
Options
Lorsque vous selectionnez un algorithme une icone
Générateur de labyrinthes
Quest permet de génerer des labyrinthes parfaits c-a-d que chaque chemin est connecté à tous les autres chemins, il n'y a donc pas de zones inaccessibles. De plus, il n'y a pas de boucles de chemin ni de murs isolés. Il y a toujours un chemin unique entre deux points quelconques du labyrinthe. Quest a plusieurs labyrinthes uniques permettent de génerer ces labyrinthes.
Amusez-vous !
Découvrez cet outil de visualisation et explorez tous les différents algorithmes.
Informations
Vous pouvez selectionner desalgorithmes de recherches dans la barre de navigation a gauche dans l'ongletAlgorithmset/ou selectionner des algorithmes de génération de labyrinthes dans l'ongletMazes and Patterns.